六甲学院中2015年(やりとり算ー★★★☆☆☆)
【六甲学院中学 2015年度 A日程】

~解説~
(1)
B君に関する情報が多いので、まずはそこに着目しましょう。
A君、B君が最初に持っていたカードの枚数をそれぞれ③枚、3⃣枚とします。
すると、1回目のやりとりは下図の様になります。

最初、B君はA君より36枚多く持っていたので、
3⃣=③+36
1回目のやりとり後、B君は66枚持っていたので、
①+2⃣=66
という、2つの条件から式が作れました。
あとは、消去算です。
3⃣=③+36 ⇒ 1⃣=①+12 ⇒ ①=1⃣-12
よって、
①+2⃣=66 ⇒ 1⃣-12+2⃣=66 ⇒ 3⃣-12=66 ⇒ 3⃣=78枚
(2)
1回目のやりとり後にC君が持っていたカードの枚数を❸枚とします。
すると、2回目のやりとりは下図の様になります。

2回目のやりとりでC君は、➊枚を渡し22枚もらうので、
❸-❶+22=46
❷+22=46
❷=24
❶=12
よって、
❸=36枚
(3)
(1)から、1⃣=26なので、
①=1⃣-12=14
③=42 ・・・A君が最初に持っていたカードの枚数
最初にC君が持っていたカードの枚数を🈪枚とします。
1回目のやりとりをまとめ直すとした図の様になります。

(2)と同様に考えて、
🈪-🈩+26=36
🈪=15 ・・・C君が最初に持っていたカードの枚数
これで、3人が最初に持っていたカードの枚数が全て分かったので、全てのやりとりをまとめ直すとした図の様になります。

よって、34枚
重要度【★★★★☆☆】
難易度【★★★☆☆☆】
 |
|
 |
|
洛南高附中2017年(回転体ー★★★★★☆)
【洛南高等学校附属中学 2017年度】

~解説~
まずは図1を回転させてできる立体を考えましょう。


上の右の図の様な、円すいを2つくっつけた立体ができますね。
この円すい1つの側面積を[1]㎠、体積を①㎤としましょう。
このとき、上右図の立体の体積Vは、
V=②㎤
となります。
また、上右図の立体の表面積Sは、円すいを2つくっつけたことで円すいの底面が表面ではなくなるので、
S=[2]㎠
となります。
(1)
いちいち立体図を描いて考える必要はありません。
平面図のまま処理する解法を習得しておきましょう。

△ABPを回転させると出来るのが円すいで、その側面積は辺ABが回転して作ったものです。
その面積が[1]㎠なので、平面図上では、辺AB=[1]㎠と表しておきましょう。
同様に、辺BQも同じ大きさの円すいの側面積を作るので、辺BQ=[1]㎠と表せます。

次に、△ACQの回転体について考えます。
△ACQを回転させても円すいが出来、その側面積は辺ACが作ったものです。
この円すいは、△ABPを回転させて作った円すいの2倍の大きさです。
よって、その側面積は、相似比の2乗になるので4倍の[4]㎠です。
平面図上では、辺AC=[4]㎠と表せます。
ここで、辺AB=[1]㎠なので、辺BC=[3]㎠となります。
同様に、辺CD=[3]㎠と表せます。

△AERの回転体も同様に考えます。
この円すいは、△ABPを回転させて作った円すいの3倍の大きさなので、側面積はその9倍の[9]㎠です。
よって、辺AE=[9]㎠となり、辺AC=[4]㎠なので、辺CE=[5]㎠と表せます。
以降も同様に考えましょう。

EF=[7]㎠、FG=[9]㎠となるので、以上をまとめると、上図が完成します。
奇数列が現れているのがポイントですね。
では、問題を解いていきましょう。

上図の様に、図2の回転体の表面積は、
[1]㎠+[1]㎠+[3]㎠+[3]㎠=[8]㎠
[8]㎠÷[2]㎠=4倍
(2)
体積についても、同じ様に考えてみましょう。

△ABPを回転させると出来るのが円すいで、その体積が①㎤なので、平面図上では△ABP=①㎤と表しておきましょう。
同様に、△QBPも同じ大きさの円すいを作るので、△QBP=①㎤と表せます。

次に、△ACQの回転体について考えます。
この円すいは、△ABPを回転させて作った円すいの2倍の大きさです。
よって、その体積は相似比の3乗になるので8倍の⑧㎤です。
平面図上では△ACQ=⑧㎤と表せ、△ABP=QBP=①㎤なので、
△BCQ=⑥㎤となります。

△AERの回転体も同様に考えます。
この円すいは、△ABPを回転させて作った円すいの3倍の大きさなので、体積はその27倍の㉗㎤です。
よって、△CED=㉗㎤ー①㎤×3-⑥㎤×2=⑫㎤と表せます。
以降も同様に考えて、まとめると下図の様になります。

では、問題を解いていきましょう。
図3の回転体の体積は、⑫㎤+⑫㎤=㉔㎤なので、
㉔㎤÷②㎤=12倍
(3)
すでに準備は完了しているので、計算するだけです。

図4の回転体の表面積は、
[1]㎠×2+[3]㎠×4+[5]㎠×2+[7]㎠×2+[9]㎠×2=[56]㎠
回転軸の逆側にもある分は、無視できることに注意しましょう。
よって、
[56]㎠÷[2]㎠=28倍
体積は、
(①㎤×2+⑥㎤×2+⑫㎤×2+⑱㎤×2+㉔㎤×2)÷②㎤=61倍
(4)
これはパズル問題です。
色々と試してみて、上手く条件を満たすような塗り方を見つけるしかありません。

(1)
重要度【★★★★☆☆】
難易度【★★★☆☆☆】
(2)
重要度【★★★☆☆☆】
難易度【★★★★☆☆】
(3)
重要度【★★★☆☆☆】
難易度【★★★★☆☆】
(4)
重要度【★☆☆☆☆☆】
難易度【★★★★★☆】
 |
|
 |
|
 |
|
明星中2020年(立体図形ー★★★★☆☆)
【明星中学 2020年度 後期】

~解説~
(1)
1階には直方体と半円柱が、2階には三角柱がありますね。
それぞれを求めて足し合わせましょう。
・直方体
3cm×8cm×10cm=240㎤
・半円柱
4cm×4cm×3.14×10cm÷2=251.2㎤
・三角柱
6cm×8cm÷2×3cm=72㎤
以上から、
240㎤+251.2㎤+72㎤=563.2㎤
(2)
切断面は、下図の様になります。

切断面の作り方(見つけ方)は、中学受験算数ではかなり難易度が高い単元ですね。
まず、切断面は点Aと点Bを通るので、その延長線上にある点Cも通ると分かります。
同様に、点Bと点Oを通るので、その延長線上にある点Dも通ります。
『平行な2面にある切断線は必ず平行になる』ので、直線ODと平行で点Cを通る直線が底面にあると分かります。
点Cは点Bの真下の点なので、点Oや点Dの真下の点である点O’や点D’を通る直線CD’が切断線です。(このとき、直線ACと直線DD’も平行になっています。)
同様に、直線ACと平行で、点Oを通る直線が三角柱の底面にあるので、点Oの真上の点である点Eも通ります。
最後に、点Aと点Eを結べば、六角形ACD’DOEが切断面だと分かります。
では、この六角形の面積を求めましょう。

OEの長さは、三角柱の底面の三角形内にある相似を利用すれば求められます。
EO:6cm=4cm:8cm
よって、EO=3cm
上図の様に、この六角形は台形と長方形を組み合わせた形なので、その面積は、
(3cm+6cm)×5cm÷2+10cm×9cm=22.5㎠+90㎠=112.5㎠
(1)
重要度【★★★★★★】
難易度【★☆☆☆☆☆】
(2)
重要度【★★★☆☆☆】
難易度【★★★★☆☆】
 |
|
 |
|
六甲学院中2017年(面積ー★★★☆☆☆)
【六甲学院中学 2017年度 B日程】

~解説~
中学受験算数の面積の問題としては、有名な問題です。
補助線の引き方が特殊なので、知識として解法を知っていないと、自力で思いつくのはやや大変でしょう。
2本の点線をどう使うかがポイントですね。
下図の様に、点Aや点Bを通り、正方形の辺と平行な線を引いてみましょう。

すると、この正方形は、下図の様に9つに分けることができます。

このとき、△APDは長方形APDIを対角線で切ったものなので、△DIAと合同で、面積が等しくなります。この面積を、◯㎠とすると、
△APD=△DIA=◯㎠
同様に、
△AMB=△BJA=▢㎠
△BNC=△CKB=◇㎠
△COD=△DLC=☆㎠
とおくことができます。
また、真ん中の長方形MNOPは、MN=5cm、NO=3cmなので、その面積は、
5cm×3cm=15㎠
正方形IJKLの面積は、
12cm×12cm=144㎠
ここで、
正方形IJKL=◯+◯+▢+▢+◇+◇+☆+☆+◎
なので、
◯+◯+▢+▢+◇+◇+☆+☆+15㎠=144㎠
◯+◯+▢+▢+◇+◇+☆+☆=144㎠ー15㎠=129㎠
◯+▢+◇+☆=129㎠÷2=64.5㎠
よって、
四角形ABCD=◯+▢+◇+☆+◎
=64.5㎠+15㎠
=79.5㎠
重要度【★★★★★☆】
難易度【★★★☆☆☆】
 |
|
 |
|
神戸女学院中2017年(点の移動ー★★★★☆☆)
【神戸女学院中学 2017年度】

~解説~
(1)
この単元は、まずは作図が必須ですね。
2秒間で、点Pは、
2cm/秒×2秒=4cm
進み、点Qは、
1cm/秒×2秒=2cm
進むので、2秒後の状態は下図の通りです。
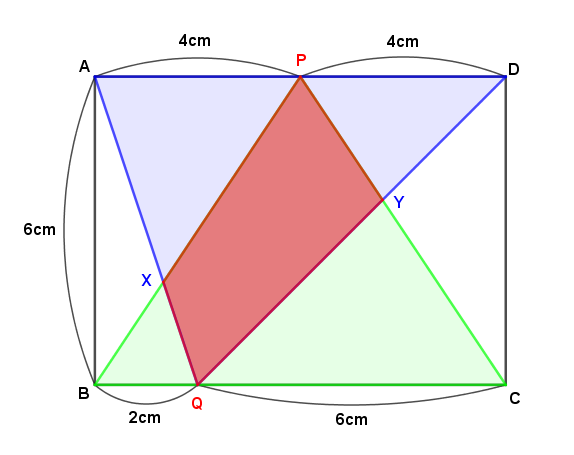
重なっている部分(赤色の部分)の面積の求め方はいくつか考えられますが、線PQで2つの三角形に切り分けてみましょう。
△BPQ=2cm×6cm÷2=6㎠
△XBQと△XPAは相似なので、
BX:PX=BQ:PA=2cm:4cm=1:2
よって、
△XPQ=△BPQ×(XP/BP)
=6㎠×(2/3)
=4㎠
△QCP=6cm×6cm÷2=18㎠
△YQCと△YDPは相似なので、
CY:PY=QC:DP=6cm:4cm=3:2
よって、
△QYP=△QCP×(PY/PC)
=18㎠×(2/5)
=7.2㎠
以上から、
4㎠+7.2㎠=11.2㎠
(2)
5秒後の状態は、下図の通りです。

本問の重なっている部分(赤色の部分)の面積の求め方もいくつか考えられます。
△ADQを基準に面積比で求めてみましょう。
△ADQ=8cm×6cm÷2=24㎠
後は、AX:XQとDY:YQが分かれば良いですね。
今の形のままでは相似が見つからないので、補助線を引いて作る必要があります。

辺ADと辺BPの延長線を引いて、その交点を点Eとしましょう。
この、相似を作る補助線の引き方は、最難関校志望生にとっては必須項目です。
△BCPと△EDPは相似なので、
BC:ED=CP:DP=4cm:2cm=2:1
よって、ED=4cm
△BQXと△EAXは相似なので、
QX:AX=BQ:EA=5cm:12cm=5:12
△BQYと△EDYは相似なので、
QY:DY=BQ:ED=5cm:4cm=5:4
以上から、
△QXY=△QAD×(QX/QA)×(QY/QD)
=24㎠×(5/17)×(5/9)
=200/51㎠
(3)
おおよその見当を付けるために、ポイントとなるタイミングごとに図を描いて面積を求めていきましょう。
ただし、点Pが辺BC上にいるとき(7~11秒後や21~25秒後など)、△BPCの面積は0㎠になるので考える必要はありません。
同様に、点Qが辺AD上にいるとき(14~22秒後など)も考えなくても良いですね。
・0秒後

0秒後の状態は上図の通りで、赤色の部分の面積は、
6cm×4cm÷2=12㎠
となり、いきなり12㎠となる時刻が見つかりました。
これを答えとしたくもなりますが、問題文に「出発してから何秒後」とあるので、0秒後は含まないと解釈して、この次に12㎠になる時刻を求めましょう。
・4秒後

点Pが点Dに到着する4秒後の状態は上図の通りです。
△BQD=4cm×6cm÷2=12㎠
△BQXと△DAXは相似なので、
BX:DX=BQ:DA=4cm:8cm=1:2
よって、
△XQD=△BQD×(XD/BD)
=12㎠×(2/3)
=8㎠
以上から、0秒後の面積が12㎠、4秒後の面積が8㎠と分かりました。
この間で、点Pと点Qの動き方は一定なので、この間の面積は、12㎠から8㎠へと減り続けることになります。
よって、この間には0秒後以外に12㎠になることはありません。
同様に、ポイントとなる時刻(点Pや点Qの動き方が変化する瞬間、つまり曲がり角に来た瞬間)を調べていきましょう。
・7秒後

7秒後の状態は上図の通りです。
このとき、点Pが辺BC上にあるので、△BPCが作れません。
よって、2つの三角形が重なる部分の面積は0㎠です。
・11秒後

・14秒後

・25秒後

以上の様に、7秒後から25秒まではずっと、2つの三角形が重なる部分の面積は0㎠です。
・28秒後

28秒後の状態は上図の通りです。
このとき、点Pと点Qが同時にスタート地点に戻ってきているので、0秒後と同じ図になっています。
2つの三角形が重なる部分の面積は12㎠で、これが0秒後の次に、初めて12㎠になる瞬間です。
よって、28秒後
(1)(2)
重要度【★★★★★☆】
難易度【★★★☆☆☆】
(3)
重要度【★★★☆☆☆】
難易度【★★★★☆☆】
 |
|
 |
|