甲陽学院中2012年(角度ー★★★☆☆☆)
【甲陽学院中学 2012年度 第二日】

~解説~
算数なのに、数字が1文字も出てこないという珍しい問題ですね。
考えられる数値は、
「三角形の内角の和」=180°
と
「一直線」=180°
ぐらいです。
『外角定理』と『ブーメラン型』を駆使して、「180°」が何個分なのかを見つけるのが基本解法です。
まずは、補助線を引いてみて、すぐに見つかる三角形を確定していきましょう。

これで180°が確定しました。
残っている角度は下図の通りですね。

下図の様に、もう1つ三角形が作れますね。

これで、2つ目の180°が確定しました。
残っている角度は下図の通りですね。

ここで、下図の様に、青線内で外角定理を使いましょう。

すると、
緑色の角度の和=赤色の角度
となるので、残っている角度は下図の様に移せます。

今度は、下図の様に、青線内でブーメラン型を使いましょう。

すると、
緑色の角度の和=赤色の角度
となるので、残っている角度は、上図の黒色の角度と赤色の角度の和になります。
これは、一直線の角度なので180°です。
以上から、全ての角度の和は、
180°×3=540°
重要度【★★★★★☆】
難易度【★★★☆☆☆】
 |
|
 |
|
||
 |
|
洛星中2019年(場合の数ー★★★☆☆☆)
【洛星中学 2019年度】

~解説~
ビンゴの問題ですね。
1列が完成したら、そこでゲーム終了になることに注意しましょう。
これぐらいの大きさなら、難しく考えずに書き出してしまう方が良いでしょう。
(ア)
1~5の欄を埋めた時点では1列が完成しておらず、1~6の欄を埋めたら1列が完成したということは、下図の様に、2段目の列に完成したということですね。

よって、「4」「5」「6」の欄は「〇」と確定します。
後は、「1」「2」「3」の欄に、1段目の列が完成しないように「〇」と「×」を入れていけばOKです。
「1」「2」「3」の欄に入る「〇」の個数で場合分けをして考えましょう。
・「〇」が0個のとき
1通り
・「〇」が1個のとき
「1」「2」「3」のどこに「〇」を入れても、残り2つが「×」ならば条件を満たします。よって、3通り。
・「〇」が2個のとき
「1」「2」「3」のどこか2つに「〇」を入れても、残り1つが「×」ならば条件を満たします。よって、3通り。
・「〇」が3個のとき
「1」「2」「3」の3か所に「〇」を3つ入れると、1段目に列が完成してしまうので条件を満たしません。よって、0通り。
以上から、
1+3+3+0=7通り
※別解
「1」「2」「3」の3か所に「〇」か「×」を入れるとき、全パターンは、
2×2×2=8通り
そのうち、「1」=「〇」、「2」=「〇」、「3」=「〇」の1パターンのみ条件を満たさないので、
8-1=7通り
(イ)
1~6の欄を埋めた時点では1列が完成しておらず、1~7の欄を埋めたら1列が完成したということは、下図の様に3パターンが考えられます。
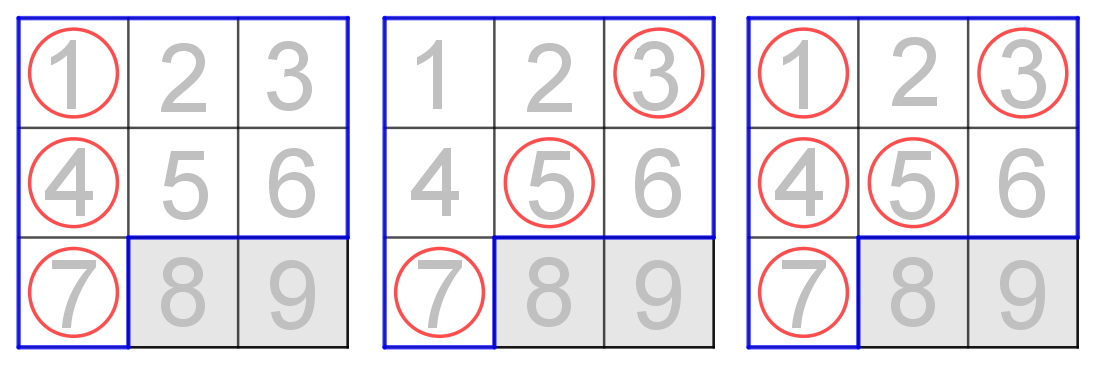
右のパターンを見落とさないように注意しましょう。
(ア)と同様に、それぞれのパターンについて「〇」の個数で場合分けをして考えていきましょう。
まずは左のパターンについて、
・「〇」が0個のとき
1通り
・「〇」が1個のとき
「2」「3」「5」「6」のどこに「〇」を入れても条件を満たすので4通り。
・「〇」が2個のとき
列が完成しないように「〇」を2個入れるには、「2」「5」、「2」「6」、「3」「6」の3通り。
・「〇」が3個のとき
列が完成しないように「〇」を3個入れることはできないので0通り。
・「〇」が4個のとき
0通り
よって、左のパターンは、
1+4+3+0+0=8通り
次に、真ん中のパターンについて、
・「〇」が0個のとき
1通り
・「〇」が1個のとき
「1」「2」「4」「6」のどこに「〇」を入れても条件を満たすので4通り。
・「〇」が2個のとき
列が完成しないように「〇」を2個入れるには、「1」「6」、「2」「4」、「2」「6」の3通り。
・「〇」が3個のとき
列が完成しないように「〇」を3個入れることはできないので0通り。
・「〇」が4個のとき
0通り
よって、左のパターンは、
1+4+3+0+0=8通り
最期に、右のパターンについて、
・「〇」が0個のとき
1通り
・「〇」が1個のとき
「2」「6」のどちらに「〇」を入れても列が完成してしまうので0通り。
・「〇」が2個のとき
0通り。
よって、右のパターンは、
1+0+0=1通り
以上から、
8+8+1=17通り
(1)
重要度【★★★★★☆】
難易度【★★☆☆☆☆】
(2)
重要度【★★★★☆☆】
難易度【★★★☆☆☆】
 |
|
 |
|
 |
|
洛南高附中2019年(相似・面積比ー★★★★☆☆)
【洛南高等学校附属中学 2019年度】

~解説~
まずは、分かることを図に書き込んでいきましょう。

具体的に分っている長さが「3cm」1つしかないので、相似で攻めるしかなさそうですね。
直角が目に付いたら、まずは「〇✖直角型相似」を探してみましょう。
三角形ABEは直角三角形なので、
∠ABE=〇° 、∠AEB=✖°
としましょう。
ここで、三角形 BCFは三角形ABEと合同なので、
∠BCF=〇° 、∠BFC=✖°
となります。
また、
∠ABC=90° 、∠ABE=〇°
なので、
∠GBC=90°ー〇°=✖°
と分かります。
よって、三角形GBCに着目すると、
∠GBC=✖° 、∠GCB=〇°
なので、
∠BGC=90°
と分かります。
また、三角形FGBも、
∠FBG=〇° 、∠FGB=90°
から、
∠BFG=✖°
となります。

以上から、
三角形ABEと三角形BCFと三角形GCBと三角形GBFが相似だと分かりました。
三角形ABEにおいて、
AE:AB=1:3
なので、三角形GCBにおいて、
GB:GC=1:3
よって、
GB=1cm
同様に、三角形GBFにおいても、
GF:GB=1:3
なので、
GF=1/3cm
よって、
FC=10/3cm
以上から、
三角形BCFの面積=10/3cm×1cm÷2=5/3㎠

三角形BFCと三角形AFCは等高三角形(底辺を辺ABとすると高さが等しい)なので、
三角形BFCの面積:三角形AFCの面積=BF:AF=1:2
よって、
三角形AFCの面積=5/3㎠×2=10/3㎠
以上から、
三角形ABCの面積=5/3㎠+10/3㎠=5㎠
よって、
正方形ABCDの面積=5㎠×2=10㎠
重要度【★★★☆☆☆】
難易度【★★★★☆☆】
 |
|
 |
|
 |
|
西大和中2019年(規則性ー★★☆☆☆☆)
【西大和学園中学 2019年度】

~解説~
4回目、5回目の図も実際に描いてみて調べましょう。
そこまでの結果を表にまとめると、下の様になります。

図形上の理屈から規則を見つけ出すのが理想ですが、中学受験算数では、数字の並びから規則を推測するのも立派な解き方です。
白と黒の個数は、2回に1回しか数字が変わっていませんね。
その数列は、
白:1,9,25・・・
黒:0,4,16・・・
となっていますが、これらの数字は『平方数(同じ数を2回かけた数)』になっていることには気付けるようにしておきましょう。
それでは、白と黒がそれぞれ31回目に何個あるかを求めましょう。
・31回目の白の個数
31÷2=15・・・1
よって、白の数列の16番目の数を求めればよいですね。
白:1(=1×1),9(=3×3),25(=5×5)・・・
なので、16番目の数は、
1+2×(16-1)=31
31×31=961
・31回目の黒の個数
黒は、最初の0だけ1回しか出てこず、それ以降は2回ずつ出てくるので、
(31-1)÷2=15・・・0
よって、黒の数列の16番目の数を求めればよいですね。
黒:0(=0×0),4(=2×2),16(=4×4)・・・
なので、16番目の数は、
0+2×(16-1)=30
30×30=900
よって、タイルは白と黒を合わせて、
961+900=1861個
※別解
合計の個数の数列から解くこともできます。
合計:1,5,13,25,41・・・
この数列は、+4,+8,+12,+16・・・
となっているので、『階差数列』です。
階差数列の解法を習得している子は、こちらから解いた方が早いですね。
4+4×(30-1)=120
1+(4+120)×30÷2=1861個
重要度【★★★★★★】
難易度【★☆☆☆☆☆】
 |
|
 |
|
 |
|
神戸女学院中2018年(面積ー★★★★☆☆)
【神戸女学院中学 2018年度】

~解説
(1)
曲線が絡む複合図形の面積を求めるときは、『曲線部分を最優先』に考えるのがポイントです。
曲線を含む図形の面積の公式は、「おうぎ形の面積の公式」しかないからです。
直線で出来ている図形の面積の公式はたくさんありますが、選択肢が多いということは、限定できないから迷うことになりますね。
本問でも、求める図形の中にある曲線がどんなおうぎ形から来ているのかを真っ先に確定させましょう。

おうぎ形の面積を求めるには、半径と中心角が必要なので、円の中心から補助線(上図の赤線)を引くのは当然ですね。
曲線部分を優先して考えると、斜線部分(上図の「あ」+「い」+「う」)の面積は、
おうぎ形「あ」+三角形「い」+おうぎ形「うえ」-三角形「え」
という方針で求めていけば良いと分かりますね。
ここで、2つのおうぎ形はともに、半径9cm、中心角30°なので、その面積は、
9cm×9cm×3.14×(30°/360°)=21.195㎠

三角形「い」は、底辺を辺ABとすると高さがCEの三角形です。
また、三角形「え」は、底辺を辺ABとすると高さがDFの三角形です。
円内の対称性に着目すると、CE=DFなので、
三角形「い」の面積=三角形「え」の面積
と分かります。
よって、求める斜線部分の面積は、
おうぎ形「あ」+おうぎ形「うえ」+三角形「い」-三角形「え」
=おうぎ形「あ」+おうぎ形「うえ」
=21.195㎠+21.195㎠
=42.39㎠
(2)
同じ様に、まずは曲線部分がどのおうぎ形から来ているかを考えます。

斜線部分が含む弧CDに関しては、おうぎ形ACDからしか求められないので、このおうぎ形は確定です。
あとは、帳じりを上手く合わせることを考えましょう。
斜線部分の面積=おうぎ形ACD+三角形ABC-三角形ABD
とすれば求められますね。
おうぎ形ACD=9cm×9cm×3.14×(60°/360°)=42.39㎠

次に、三角形の面積を考えましょう。
三角形ABCに関しては、
AE=9cm
∠EAB=60°
円内の対称性に着目して、
∠ABE=90°
よって、『30°-60°-90°の直角三角形の法則』から、
AB=9cm÷2=4.5cm
∠BAC=90°
AC=9cm
よって、
三角形ABC=4.5cm×9cm÷2=20.25㎠
三角形ABDに関しては、底辺を辺ABにすると、高さはDFの長さです。
ここで、三角形ADFも30°-60°-90°の直角三角形なので、
AD=9cmから、DF=9cm÷2=4.5cm
よって、
三角形ABD=4.5cm×4.5cm÷2=10.125㎠
以上から、
斜線部分の面積=42.39㎠+20.25㎠ー10.125㎠
=52.515㎠
(1)
重要度【★★★★☆☆】
難易度【★★★☆☆☆】
(2)
重要度【★★★★☆☆】
難易度【★★★★☆☆】
 |
|
 |
|